问题
计算题
∣m+4 ∣与n2-2n+1互为相反数，把多项式x2+4y2-mxy-n分解因式
答案
解：由题意可得：∣m+4 ∣+ n2-2n+1=0
即 ∣m+4∣+（n-1）2=0
所以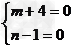 
解得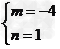
所以x2+4y2-mxy-n= x2+4y2+4xy-1
=(x+2y)2-1
=(x+2y+1)(x+2y-1)
搜题请搜索小程序“爱下问搜题”
∣m+4 ∣与n2-2n+1互为相反数，把多项式x2+4y2-mxy-n分解因式
解：由题意可得：∣m+4 ∣+ n2-2n+1=0
即 ∣m+4∣+（n-1）2=0
所以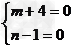
解得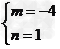
所以x2+4y2-mxy-n= x2+4y2+4xy-1
=(x+2y)2-1
=(x+2y+1)(x+2y-1)