问题
问答题
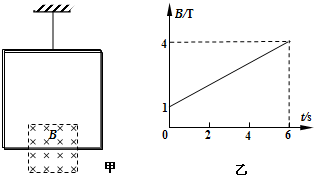
轻质细线吊着一质量为m=0.32kg,边长为L=0.8m、匝数n=10的正方形线圈总电阻为r=1Ω.边长为
的正方形磁场区域对称分布在线圈下边的两侧,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经t0时间细线开始松驰,g=10m/s2.求:L 2
(1)在前t0时间内线圈中产生的电动势;
(2)在前t0时间内线圈的电功率;
(3)求t0的值.
答案
(1)由法拉第电磁感应定律得:ε=n
=n△φ △t
(1 2
)2L 2
=10×△B △t
(1 2
)2×0.5=0.4(V)0.8 2
故在前t0时间内线圈中产生的电动势为0.4V.
(2)I=
=0.4Aε r
P=I2r=0.16(W)
故在前t0时间内线圈的电功率为0.16W.
(3)分析线圈受力可知,当细线松弛时有:F安=nBtI
=mgL 2
I=ε r
Bt=
=2T2mgr n?L
由图象知:Bt =1+0.5t0解得:t0=2s
故t0的值为2s.
