问题
解答题
求证:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
答案
已知,在Rt△ABC中,∠A=30°,∠ACB=90°.
求证:BC=
AB.1 2
证明:
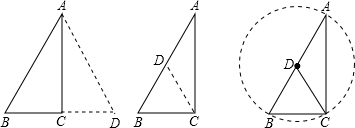
证法一:如答图所示,延长BC到D,使CD=BC,连接AD,易证AD=AB,∠BAD=60°.
∴△ABD为等边三角形,
∴AB=BD,
∴BC=CD=
AB,即BC=1 2
AB.1 2
证法二:如答图所示,取AB的中点D,
连接DC,有CD=
AB=AD=DB,1 2
∴∠DCA=∠A=30°,∠BDC=∠DCA+∠A=60°.
∴△DBC为等边三角形,
∴BC=DB=
AB,即BC=1 2
AB.1 2
证法三:如答图所示,在AB上取一点D,使BD=BC,
∵∠B=60°,
∴△BDC为等边三角形,
∴∠DCB=60°,∠ACD=90°-∠DCB=90°-60°=30°=∠A.
∴DC=DA,即有BC=BD=DA=
AB,1 2
∴BC=
AB.1 2
证法四:如图所示,作△ABC的外接圆⊙D,∠C=90°,AB为⊙O的直径,
连DC有DB=DC,∠BDC=2∠A=2×30°=60°,
∴△DBC为等边三角形,
∴BC=DB=DA=
AB,即BC=1 2
AB.1 2