问题
选择题
直角三角形的周长为2+
|
答案
∵CD是直角三角形ABC斜边上的中线,
∴AB=2CD=2,
∵直角三角形ABC的周长是2+
,6
∴AC+BC=
,6
两边平方得:AC2+2AC•BC+BC2=6,
由勾股定理得:AC2+BC2=AB2=4,
∴2AC•BC=2,
AC×BC=1,
∴S△ABC=
AC×BC=1 2
1=1 2
.1 2
故选B.
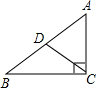
直角三角形的周长为2+
|
∵CD是直角三角形ABC斜边上的中线,
∴AB=2CD=2,
∵直角三角形ABC的周长是2+
,6
∴AC+BC=
,6
两边平方得:AC2+2AC•BC+BC2=6,
由勾股定理得:AC2+BC2=AB2=4,
∴2AC•BC=2,
AC×BC=1,
∴S△ABC=
AC×BC=1 2
1=1 2
.1 2
故选B.
