问题
填空题
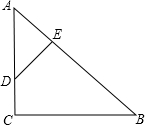
在等腰Rt△ABC中,∠C=90°,AC=BC,点D在AC边上,DE⊥AB,垂足为E,AD=2DC,则S△ADE:S四边形DCBE的值为______.
答案
根据题意画出图形,如图所示,
∵△ABC为等腰直角三角形,DE⊥AB,
∴∠C=∠AED=90°,AC=BC,
由AD=2DC,设AD=2,DC=1,则AC=3,
根据勾股定理得:AB=3
,2
∵∠A=∠A,
∴△AED∽△ACB,
∴
=AD AB
,2 3 2
∴S△ADE:S△ABC=4:18=2:9,
则S△ADE:S四边形DCBE的值为
.2 7
故答案为:2 7