已知△ABC中，AB=AC=2，∠BAC=90°，直角∠EPF的顶点P是BC的中

问题填空题

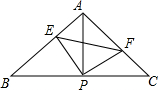
已知△ABC中，AB=AC=2，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：①AE=CF；②tan∠PEF=

；③S_△EPF的最小值为

；④S_{四边形AEPF}=1．当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），上述结论中始终正确的有______．

答案

∵∠APE、∠CPF都是∠APF的余角，

∴∠APE=∠CPF，

∵AB=AC，∠BAC=90°，P是BC中点，

∴AP=CP，

又∵AP=CP，∠EPA=∠FPC，

∴△APE≌△CPF（ASA），同理可证△APF≌△BPE，

∴AE=CF（故①正确），△EPF是等腰直角三角形（最小值为1，tan∠PEF=1，故②错误③正确），S_{四边形AEPF}=

S_△ABC=1（故④正确），①③④正确；

故答案为：①③④．