利用单摆验证小球平抛运动规律,设计方案如图(a)所示,在悬点O正下方有水平放置的炽热的电热丝P,当悬线摆至电热丝处时能轻易被烧断;MN为水平木板,已知悬线长为L,悬点到木板的距离OO′=h(h>L).
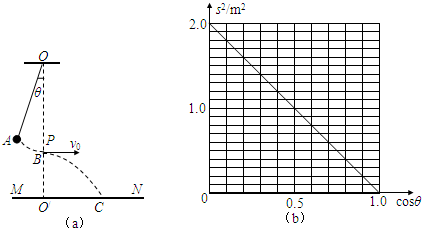
(1)电热丝P必须放在悬点正下方的理由是:______.
(2)将小球向左拉起后自由释放,最后小球落到木板上的C点,O′C=s,则小球做平抛运动的初速度为v0=______.
(3)在其他条件不变的情况下,若改变释放小球时悬线与竖直方向的夹角θ,小球落点与O′点的水平距离s将随之改变,经多次实验,以s2为纵坐标、cosθ为横坐标,得到如图(b)所示图象.则当θ=30?时,s为______m;若悬线长L=1.0m,悬点到木板间的距离OO′为______m.
(1)由于在烧断细线前小球做圆周运动,故速度方向沿切线方向,所以只有在悬点正下方物体的速度沿水平方向,要小球做平抛运动,则小球平抛的初速度只能沿水平方向,故只有保证小球沿水平方向抛出才能保证物体做平抛运动.(2)由于小球做平抛运动故有在水平方向有s=vt
在竖直方向有h-L=
gt2…①1 2
故有v=s
; g 2(h-L)
(3)变释放小球时悬线与竖直方向的夹角θ时,小球平抛的速度v,则有mg(L-Lcosθ)=
mv2…②1 2
则物体在水平方向的位移s=vt…③
联立①②③可得
s2=4(h-L)L(1-cosθ)
显然当cosθ=0时,即有2=4(h-L)L(1-cosθ)
当θ=30°时,cosθ=
,s2=4(h-L)L(1-3 2
)3 2
故有
=2 s2
=1 1- 3 2 2 2- 3
故s=
=2- 3
=0.52m.0.268
s2=4(h-L)L(1-cosθ)
故当l=1.0m时有:2=4(h-1)×1,
即h-1=0.5
h=1.5.
故答案为(1)保证小球沿水平方向抛出.
(2)s
; g 2(h-L)
(3)0.52,1.5.
