问题
填空题
已知△ABC中∠ACB=90°,CD⊥AB于D,∠A=30°,BC=2cm,则AD=______.
答案
∵△ABC中∠ACB=90°,∠A=30°,BC=2cm,
∴AB=2BC=4cm,∠B=60°,
∵DC⊥AB,
∴∠CDB=90°,
∴∠DCB=30°,
∴BD=
BC=1cm,1 2
∴AD=AB-BD=4cm-1cm=3cm,
故答案为:3cm.
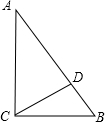
已知△ABC中∠ACB=90°,CD⊥AB于D,∠A=30°,BC=2cm,则AD=______.
∵△ABC中∠ACB=90°,∠A=30°,BC=2cm,
∴AB=2BC=4cm,∠B=60°,
∵DC⊥AB,
∴∠CDB=90°,
∴∠DCB=30°,
∴BD=
BC=1cm,1 2
∴AD=AB-BD=4cm-1cm=3cm,
故答案为:3cm.
