问题
解答题
⊙O2与⊙O1交于A,B两点,射线O1A交⊙O2于C点,射线O2A交⊙O1于D点.求证:点A是△BCD的内心.
答案
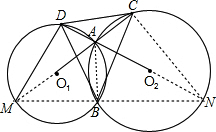
证明:设两圆为⊙O、⊙Q,如图
延长CA交⊙O1于M点,延长DA交⊙O2于N点,连接AB、DM、CN、MN,
∵AM是⊙O1的直径,AN是⊙O2的直径,
∴∠MDN=∠ACN=90°,
∴C、D、M、N四点共圆,
∴∠DMC=∠DNC,
∵∠DMC=∠DBA,∠DNC=∠ABC,
∴∠DBA=∠ABC,
∴点A在∠DBC的角平分线上,
∵C、D、M、N四点共圆,
∴∠DCM=∠DNM,
∵∠DNM=∠ACB,
∴∠DCM=∠ACB,
∴点A在∠DCB的角平分线上,
同理:点A在∠CDB的角平分线上,
∴点A是△CDB的三个角平分线的交点,
∴点A是△BCD的内心.