问题
解答题
求证：三角形两边的积等于其外接圆的直径与第三边的高的积．
答案
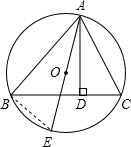
已知：⊙O是△ABC的外接圆，AD是△ABC中BC边上的高，AE是⊙O直径．
求证：AB?AC=AD?AE．
证明：连BE．AE是直径，∠ABE=90°，
AD⊥BC，∠ADC=90°，∠ABE=∠ADC，∠C=∠E，
△ADC∽△ABE，
=AC AE
，AD AB
即AB?AC=AD?AE．
．
搜题请搜索小程序“爱下问搜题”