问题
填空题
若一三角形的三边长分别为5、12、13,则此三角形的内切圆半径为______.
答案
∵AC2+BC2=25+144=169,AB2=169,
∴AC2+BC2=AB2,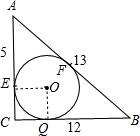
∴∠C=90°,
连接OE、OQ,
∵圆O是三角形ABC的内切圆,
∴AE=AF,BQ=BF,∠OEC=∠OQC=∠C=90°,OE=OQ,
∴四边形OECQ是正方形,
∴设OE=CE=CQ=OQ=a,
∵AF+BF=13,
∴12-a+5-a=13,
∴a=2,
故答案为:2.
