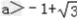问题
解答题
设集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}
（1）若A∩B={2}，求实数a的值；
（2）若A∪B=A，求实数a的取值范围；
（3）若U=R，A∩（CUB）=A，求实数a的取值范围．
答案
解：（1）∵A∩B={2}，∴2∈B，
代入B中方程得a2+4a+3=0，
所以a=﹣1或a=﹣3
当a=﹣1时，B={﹣2，2}，满足条件；
当a=﹣3时，B={2}，也满足条件综上得a的值为﹣1或﹣3；
（2）∵A∪B=A，∴B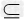
A
①当△=4（a+1）2﹣4（a2﹣5）=8（a+3）＜0，即a＜﹣3时，B=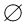
满足条件
②当△=0即a=﹣3时，B={2}，满足要求
③当△＞0，即a＞﹣3时，B=A={1，2}才能满足要求，不可能
故a的取值范围是a≤﹣3．
（3）∵A∩（CUB）=A，
∴A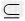
（CUB），
∴A∩B=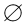
①当△＜0，即a＜﹣3时，B=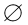
，满足条件
②当△=0即a=﹣3时，B={2}，A∩B={2}不适合条件
③当△＞0，即a＞﹣3时，
此时只需1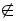
B且2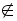
B 将2代入B的方程得a=﹣1或a=﹣3 将1代入B的方程得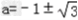
∴ 
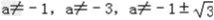
综上，a的取值范围是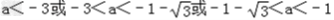 
或
或 