问题
填空题
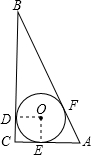
已知Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,则△ABC的内切圆半径为______cm.
答案
连接OD、OE,
∵⊙O是△ACB的内切圆,
∴BD=BF,AE=AF,CD=CE,∠ODC=∠C=∠OEC=90°,
∵OD=OE,
∴四边形DCEO是正方形,
∴OD=DC=OE=CE,
∵在Rt△BCA中,由勾股定理得:AB=
=13(cm),52+122
∴BF+AF=BD+AE=12-OD+5-OE=13,
∴OD=OE=2(cm),
故答案为:2.