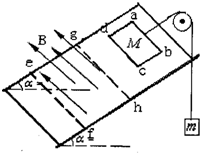
如图所示,光滑斜面的倾角θ=30°,在斜面上放置一矩形线框abcd,ab边的边长为1m,bc边的边长为0.8m,线框的质量M=4kg,电阻为0.1Ω,线框通过细线绕过光滑的定滑轮与重物相连,滑轮的质量不计,重物的质量m=lkg,斜面上ef和曲线为斜面上有界匀强磁场的边界,与斜面的底边平行,ef和曲线的间距为1.8m,磁场方向垂直于斜面向上,B=0.5T,开始cd边离gh边的距离为2.25m,由静止释放,线框恰好能匀速穿过ef边界,线框滑动过程中cd边始终与底边平行,求:(设斜面足够长,重物m不会与滑轮接触,g取10m/s2)
(1)线框cd边刚进入磁场时速度的大小.
(2)线框进入磁场过程中通过线框的电量.
(3)线框进入磁场过程中在线框中产生的焦耳热.
(1)设M下落的高度h1=2.25×sin30°m,m上升的高度h2=2.25m.则M和m系统机械能守恒,则:
Mgh1-mgh2=
(M+m)v2 ①1 2
线框刚进入磁场时的速度:v=3m/s. ②
(2)线框进入磁场的过程中产生的感应电流的平均值为I,磁通量的变化量为△Φ,变化的时间为△t,感应电动势为E,通过线框的电荷量为q,则有:
q=I△t ③
I=
④E R
E=
⑤△Φ △t
由③④⑤式得,q=4C. ⑥
(3)当线框在匀速穿过ef边界时,设速度为v1,由平衡知:
Mgsinα-mg-BIL=0 ⑦
I=
⑧BLv1 R
由⑦⑧式得,v1=4m/s.⑨
设线框完全进入磁场时的速度为v2,下滑高度为H,重物上升的高度为 h,则:
MgH-mgh=
(m+M)v12-1 2
(m+M)v22 ⑩1 2
得v2=2
m/s.3
从线框开始进入磁场到完全进入磁场的过程中,下滑的高度为H1,重物上升的高度为h3.此过程线框产生的焦耳热为Q′,由功能关系得,
(m+M)v22-1 2
(m+M)v2=MgH1-mgh3-Q′1 2
得Q′=0.5J.
答:(1)线框cd边刚进入磁场时速度的大小为3m/s.
(2)线框进入磁场过程中通过线框的电量为4C.
(3)线框进入磁场过程中在线框中产生的焦耳热为0.5J.
