问题
选择题
正三角形的内切圆半径为1,那么这个正三角形的边长为( )
|
答案
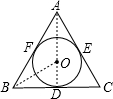
如图,⊙O是△ABC的内切圆,⊙O切AB于F,切AC于E,切BC于D,
连接AD,OB,则AD过O(因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),
∵△ABC是等边三角形,
∴∠ABC=60°,
∵⊙O是△ABC的内切圆,
∴∠OBC=
∠ABC=30°,1 2
∵⊙O切BC于D,
∴∠ODB=90°,
∵OD=1,
∴OB=2,
由勾股定理得:BD=
=22-12
,3
同理求出CD=
,3
即BC=2
.3
故选D.