问题
填空题
已知⊙O是等边三角形ABC的内切圆，⊙O的半径为1，则等边三角形ABC的边长为______．
答案
连接OB，OD，
∵⊙O是等边△ABC的内切圆，
∴∠OBD=30°，∠BDO=90°，
∴OB=2OD=2，
由勾股定理得：BD=
=OB2-OD2
，3
同理CD=
，3
∴BC=BD+CD=2
，3
故答案为：2
．3
搜题请搜索小程序“爱下问搜题”
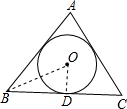
已知⊙O是等边三角形ABC的内切圆，⊙O的半径为1，则等边三角形ABC的边长为______．
连接OB，OD，
∵⊙O是等边△ABC的内切圆，
∴∠OBD=30°，∠BDO=90°，
∴OB=2OD=2，
由勾股定理得：BD=
=OB2-OD2
，3
同理CD=
，3
∴BC=BD+CD=2
，3
故答案为：2
．3