问题
选择题
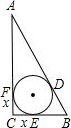
⊙O是△ABC的内切圆,且∠C=90°,切点为D,E,F,若AF,BE的长是方程x2-13x+30=0的两个根,则S△ABC的值为( )
A.30
B.15
C.60
D.13
答案
如图;
解方程x2-13x+30=0,得:
x=10,x=3,
∴AD=AF=10,BD=BE=3;
设CE=CF=x,则AC=10+x,BC=3+x;
由勾股定理,得:
AB2=AC2+BC2,即132=(10+x)2+(3+x)2,
解得:x=2(负值舍去),
∴AC=12,BC=5;
因此S△ABC=
AC•BC=1 2
×5×12=30.1 2
故选A.