问题
单项选择题
在区间(-∞,+∞)内,方程
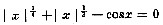
答案
参考答案:C
解析:
[分析]: 设[*]f(x)是偶函数,只须考察f(x)在[0,+∞)内零点的个数.
当x>0时,[*]
又当[*]
这表明[*]时,f(x)没有零点.所以只须考虑f(x)在[*]内零点的个数,又[*]当[*]时,f'(x)>0,所以f(x)在[*]内单调递增,因而f(x)在[*]内至多有一个零点.[*],由连续函数的零点存在定理,在[*]内f(x)存在零点.综合上述,f(x)在[0,+∞)内存在唯一零点,于是可得方程f(x)=0在(-∞,+∞)内有且仅有两个实根.应选(C).
