问题
单项选择题
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解,α1,α2是对应齐次线性方程组Ax=0的基础解系,k1,k2为任意常数,则方程组Ax=b的通解必是
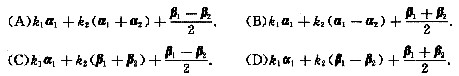
答案
参考答案:B
解析:
[分析]: 由α1,α2是齐次线性方程组Ax=0的基础解系知n-r(A)=2,从而非齐次线性方程组Ax=b的通解形式为:k1η1+k2η2+ξ.其中η1,η2是Ax=0的基础解系,ξ是Ax=b的解.
由方程组解的性质知[*]都是Ax=0的解,[*]是Ax=b的解.
那么(A)中没有方程组Ax=b的特解ξ,(C)中没有特解ξ而且β1+β2也不是齐次方程组Ax=0的解,(D)中虽有特解ξ,但齐次方程组α1,β1-β2的线性无关性没有保证.
唯(B)中,不仅α1,α1-α2是Ax=0的解而且是线性无关的,同时[*]是Ax=b的解,故应选(B).
