问题
选择题
在Rt△ABC，AB=AC=2，∠BAC=90°，能完全覆盖住此三角形的最小圆的面积是（ ）
A．π
B．2π
C．3π
D．4π
答案
如图，∵∠C=90°，
∴能完全覆盖住△ABC的最小圆为以AB为直径的圆，
由勾股定理，得AB=
=2AC2+BC2
，2
∴圆的半径为
，面积为：π（2
）2=2π．2
故选B．
搜题请搜索小程序“爱下问搜题”
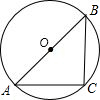
在Rt△ABC，AB=AC=2，∠BAC=90°，能完全覆盖住此三角形的最小圆的面积是（ ）
A．π
B．2π
C．3π
D．4π
如图，∵∠C=90°，
∴能完全覆盖住△ABC的最小圆为以AB为直径的圆，
由勾股定理，得AB=
=2AC2+BC2
，2
∴圆的半径为
，面积为：π（2
）2=2π．2
故选B．