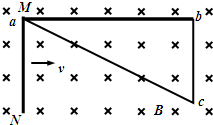
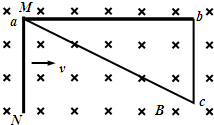
如图所示,直角三角形导线框abc固定在匀强磁场中,ab是一段长为l1=0.6m、单位长度电阻为r=3Ω/m的均匀导线,ac和bc的电阻可不计,bc长度为l2=0.3m.磁场的磁感强度为B=0.5T,方向垂直纸面向里.现有一段长度为L=0.3m、单位长度电阻也为r=3Ω/m的均匀导体杆MN架在导线框上,开始时紧靠a点,然后沿ab方向以恒定速度v=1.2m/s向b端滑动,滑动中始终与bc平行并与导线框保持良好接触.
(1)导线框中有感应电流的时间是多长?
(2)当导体杆MN滑到ab中点时,导线bc中的电流多大?方向如何?
(3)求导体杆MN自a点至滑到ab中点过程中,回路中感应电动势的平均值.
(4)找出当导体杆MN所发生的位移为x(0<x≤0.6m)时,流经导体杆的电流表达式;并求当x为何值时电流最大,最大电流是多少?
(1)导线框中有感应电流的时间为t==s=0.5s
(2)当MN滑到ab中点时,R外=Ω=0.45Ω,r内=0.15×3Ω=0.45Ω,R总=0.9Ω
感应电动势ε=BLv=×0.5×0.3×1.2V=0.09V
根据闭合电路欧姆定律得:I==A=0.1A
所以Ibc=I=×0.1A=0.05A
方向b指向c;
(3)回路中感应电动势的平均值为====0.045V
或==V=0.045V
(4)当MN运动距离为x时,有ε′=B••v,
r′=r,R外==r
I总====
代入数据,得I总=(A)(0<x≤0.6m)
可见,当x=0.6m时,导体杆中电流最大,最大电流为Im=A=0.2A