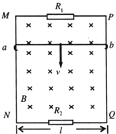
如图所示,MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计.导轨所在平面与磁感应强度B=5.0T的匀强磁场垂直.质量m=6.0×10-2kg、电阻r=0.5Ω的金属杆ab始终垂直于导轨,并与其保持光滑接触.导轨两端分别接有阻值均为3.0Ω的电阻R1和R2.重力加速度取10m/s2,且导轨足够长,若使金属杆ab从静止开始下滑,求:
(1)杆下滑的最大速率vm;
(2)稳定后整个电路耗电的总功率P;
(3)杆下滑速度稳定之后电阻R2两端的电压U.
(1)已知ab杆的电阻r=0.5Ω,R1和R2并联的总电阻为R=1.5Ω,电路的总电阻 r+R=2.0Ω
ab杆匀速下滑时,产生的感应电动势 ɛ=Blvm
感应电流 I=ɛ R+r
∴ab杆所受的安培力 F=BIl=B2l2vm R+r
又由平衡条件得 mg=F
∴联立解得 vm=
=0.3m/smg(R+r) B2l2
(2)由能量转化和守恒定律有:P=mgvm=0.18W
(3)通过ab杆的电流 I=
=0.3ABlvm R+r
∴R2两端的电压 U=IR=0.45V
答:
(1)杆下滑的最大速率vm为0.3m/s.
(2)稳定后整个电路耗电的总功率P为0.18W;
(3)杆下滑速度稳定之后电阻R2两端的电压U为0.45V.
