问题
问答题
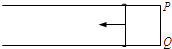
如图所示,两根平行金属导轨固定在水平桌面上,每根导轨每米的电阻为r0=0.10Ω/m,导轨的端点P、Q用电阻可以忽略的导线相连,两导轨间的距离l=0.20m.有随时间变化的匀强磁场垂直于桌面,已知磁感应强度B与时间t的关系为B=kt,比例系数k=0.020T/s.一电阻不计的金属杆可在导轨上无摩擦低滑动,在滑动过程中保持与导轨垂直.在t=0时刻,金属杆紧靠在P、Q端,在外力作用下,杆以恒定的加速度从静止开始向导轨的另一端滑动,求在t=6.0s时金属杆所受的安培力.
答案
用a表示金属杆的加速度,在t时刻,金属杆与初始位置的距离L=
at2,1 2
此时杆的速度v=at,
这时,杆与导轨构成的回路的面积S=Ll,回路中的感应电动势
E=S
+Blv=Sk+Blv,△B △t
回路总电阻R=2Lr0,
回路感应电流I=
,作用于杆的作用力F=BlI,E R
解得F=
t,3k2l2 2r0
带入数据得F=1.44×10-3N
答:在t=6.0s时金属杆所受的安培力是1.44×10-3N
