如图所示,两根相距L=0.5m的平行金属足够长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,分界线O1O2右侧为磁感应强度B1=0.6T方向竖直向上的匀强磁场,左侧为磁感应强度为B2=0.4T方向竖直向下的匀强磁场,导轨上横放着两条金属细杆,构成矩形闭合回路,每条金属细杆的质量m=0.2kg,电阻为R=1.5Ω,回路中其余部分电阻可不计.开始时,ef速度为0,给cd一个大小为v0=2.6m/s水平向右的初速度,不计金属细杆与导轨之间的摩擦且接触良好.求:
(1)金属细杆ef的最大加速度.
(2)金属细杆,ef的最大速度.
(3)通过金属细杆ef的最多电荷量.
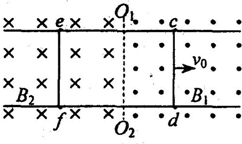
(1)当cd棒向右运动时,产生感应电流,ef棒会受到向左的安培力作用,ef棒向左加速运动,也切割磁感线,产生感应电动势,ef的感应电动势与cd棒的感应电动势方向相反,使回路中感应电流减小,ef棒所受的安培力减小,加速度减小,所以开始时,ef的加速度最大.
感应电动势 E0=B1Lv0,感应电流为I0=E0 2R
则得ef所受的安培力为F0=B2IL=B1B2L2v0 2R
故金属细杆ef的最大加速度为amax=
=F0 m B1B2L2v0 2mR
代入数据解得,amax=0.26m/s2
(2)、(3)ef先做加速度减小的变加速运动,cd棒做减速运动,当两棒的感应电动势大小相等时,回路中感应电流为零,两棒不再受安培力,都做匀速直线运动,ef速度达到最大.设金属细杆ef的最大速度大小为v2,此时cd杆的速度大小为v1.
则有
B1Lv1=B2Lv2,
根据动量定理得:
对cd杆:-B1
Lt=mv1-mv0,. I
对ef杆:B2
Lt=mv2,. I
又 电量Q=
t. I
代入解得:v2=1.2m/s,Q=1.2C
答:
(1)金属细杆ef的最大加速度为0.26m/s2.
(2)金属细杆,ef的最大速度为1.2m/s.
(3)通过金属细杆ef的最多电荷量为1.2C.
