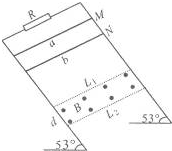
如图所示,两根足够长且平行的光滑金属导轨与水平面成530角放置,导轨间接一阻值为3Ω的电阻R,导轨电阻忽略不计.在两平行虚线L1、L2间有一与导轨所在平面垂直、磁感应强度为B的匀强磁场,磁场区域的宽度为d=0.5m.导体棒a的质量为ma=0.2kg,电阻Ra=3Ω;导体棒b的质量为mb=0.1kg,电阻Rb=6Ω;它们分别垂直导轨放置并始终与导轨接触良好,现从图中的M、N处同时将它们由静止开始释放,运动过程中它们都能匀速穿过磁场区域,当b刚穿出磁场时,a正好进入磁场.取重力加速度g=10m/s2,sin53°=0.8且不计a、b之间电流的相互作用,求:
(1)在整个过程中,a、b两导体棒分别克服安培力做的功;
(2)在a穿越磁场的过程中,a、b两导体棒上产生的焦耳热之比;
(3)M点和N点之间的距离.
(1)对a杆:由于金属杆匀速穿过磁场,所以穿过的过程中受力平衡:
即:F安a=magsin53°
克服安培力做功的大小与重力做的功大小相同
即:Wa=magsin53°×d=0.8J
对b杆:由于金属杆匀速穿过磁场,所以穿过的过程中受力平衡:
即:F安b=mbgsin53°
克服安培力做功的大小与重力做的功大小相同
即:Wb=mbgsin53°×d=0.4J
(2)在a穿越磁场过程中,a杆是电源,b与R是外电路:Ia=Ib+IR ①
b与R并联电压相同:IbRb=IRR,解得:Ib=IR 2
把结果代入①解得:
=3Ia Ib
则:
=Qa Qb
=
RatI 2a
RbtI 2b 9 2
(3)设b在磁场中匀速运动的速度为vb,则b中的电流:Ib=BLvb R总1
电路的总电阻:R总1=7.5Ω
由b杆受力平衡得:BIbL=
=mgsin53° ②B2L2vb R总1
同理a棒在磁场中匀速运动时总电阻:R总2=5Ω
=magsin53° ③B2L2va R总2
由②③两式取比值得:vb:va=3:4
根据题意得:va=vb+gsin53°•t
d=vb•t
由位移速度关系式:v2=2gsin53°•x
由上式整理,M点和N点距L1的距离:xa=
m xb=4 3
m3 4
所以:xMN=xa-xb=
m7 12
答:(1)在整个过程中,a、b两导体棒分别克服安培力做的功为0.8J,0.4J;
(2)在a穿越磁场的过程中,a、b两导体棒上产生的焦耳热之比9:2;
(3)M点和N点之间的距离为
m.7 12
