问题
选择题
如图所示,间距为L、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m、电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中.现使金属棒以初速度v沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )
A.金属棒在导轨上做匀减速运动
B.整个过程中金属棒在导轨上发生的位移为qR BL
C.整个过程中金属棒克服安培力做功为
mv21 2
D.整个过程中电阻R上产生的焦耳热为1 2mv2 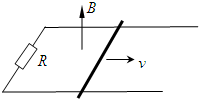
答案
A、金属棒切割产生感应电动势,产生感应电流,从而受到向左的安培力,做减速运动,由于速度减小,电动势减小,则电流减小,安培力减小,根据牛顿第二定律知,加速度减小,做加速度逐渐减小的减速运动.故A错误.
B、根据q=
=△Φ R总
,则金属棒在导轨上发生的位移s=BLs 2R
.故B错误.2qR BL
C、根据动能定律得,-WA=0-
mv2,则金属棒克服安培力做功为1 2
mv2.故C正确.1 2
D、根据能量守恒得,动能的减小全部转化为整个回路产生的热量,则电阻R产生的热量QR=
mv2.故D错误.1 4
故选C.
