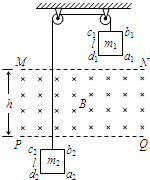
如图所示,一正方形平面导线框a1b1c1d1,经一条不可伸长的绝缘轻绳与另一正方形平面导线框a2b2c2d2相连,轻绳绕过两等高的轻滑轮,不计绳与滑轮间的摩擦.两线框位于同一竖直平面内,a1d1边和a2d2边是水平的.两线框之间的空间有一匀强磁场区域,该区域的上、下边界MN和PQ均与a1d1边及a2d2边平行,两边界间的距离为h=78.40cm.磁场方向垂直线框平面向里.已知两线框的边长均为l=40.00cm,线框a1b1c1d1的质量为m1=0.40kg,电阻为R1=0.80Ω.线框a2b2c2d2的质量为m2=0.20kg,电阻为R2=0.40Ω.现让两线框在磁场外某处开始释放,两线框恰好同时以速度v=1.20m/s匀速地进入磁场区域,不计空气阻力,重力加速度取g=10m/s2.求:
(1)在图25上标出两线框同时进入磁场时,线框a1b1c1d1中的感应电流方向和线框a2b2c2d2所受到的安培力的方向;
(2)磁场的磁感应强度B的大小;
(3)a1d1边刚穿出磁场时,线框a1b1c1d1中电流强度的大小.
(1)根据楞次定律判断可知,线框a1b1c1d1中的感应电流方向沿逆时针,线框a2b2c2d2中的感应电流方向沿逆时针,由
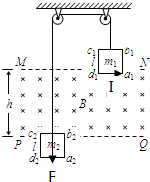
左手定则判断可知线框a2b2c2d2所受到的安培力的方向向下.
(2)两线框中的感应电流分别为 I1=
=E R1 Blv R1
I2=
=E R2 Blv R2
a1d1边及b2c2边受到的安培力大小分别为 F1=BI1l
F2=BI2lF2=2F1
设此时轻绳中的拉力为T,两线框处于平衡状态,有 m1g-F1-T=0
T-F2-m2g=0
由以上各式,解得 B=
=1.67T(m1-m2)gR1R2 l2v(R1+R2)
(3)当两线框完全在磁场中时,两线框中均无感应电流,两线框均做匀加速运动,设线框的a1d1边 b2c2边刚穿出磁场时两线框的速度大小为v',由机械能守恒定律,得 (m1-m2)g(h-l)=
(m1+m2)v′2-1 2
(m1+m2)v21 2
代入数据得,v'=2m/s.
设a1d1边刚穿出磁场时,线框a1b1c1d1中的电流强度的大小为I,则 I=
=1.67ABlv′ R1
答:
(1)线框a1b1c1d1中的感应电流方向和线框a2b2c2d2所受到的安培力的方向如图所示;
(2)磁场的磁感应强度B的大小为1.67T;
(3)a1d1边刚穿出磁场时,线框a1b1c1d1中电流强度的大小为1.67A.
