问题
计算题
如图，轻直杆AB长为2m，两端各连着一个质量为1kg的小球，直杆绕着O点以ω=8rad/s逆时针匀速转动，AO=1.5m，A轨迹的最低点时恰好与一个直角斜面体的顶点相切，斜面的底角为37°和53°，取g=10m/s2。
（1）当A球通过最低点时，求B球对直杆的作用力；
（2）若当A球通过最低点时，两球脱离轻杆（不影响两球瞬时速度，此后两球不受杆影响），此后B球恰好击中斜面底部，且两球跟接触面碰后不反弹，试求B在空中飞行的时间；
（3）在（2）的情形下，求两球落点间的距离。
答案
解：（1）设杆对B球的作用力F向下，有
解得F=22N，即杆对B的作用力为22N，方向向下
由牛顿第三定律，B球对杆的作用力F'=8N，方向向上
（2）脱离轻杆时vA=ωOA=12m/s，vB=ωOB=4m/s
设在空中飞行时间为t，则有：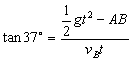
解得合理根t=1s
（3）B的水平位移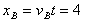
m
A的水平位移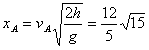
m＞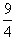
m，直接落在地面上
因此两球落点间距为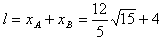
m