如图所示,相距为L的平行金属导轨ab、cd与水平面成θ角放置,导轨与阻值均为R的两定值电阻R1、R2相连,磁感应强度为B的匀强磁场垂直穿过导轨平面.有一质量为m、阻值也为R的导体棒MN,以速度v沿导轨匀速下滑,它与导轨之间的动摩擦因数为μ,忽略感应电流之间的相互作用,则( )
A.导体棒下滑的速度大小为mgR(sinθ-μcosθ) B2L2
B.电阻R1消耗的热功率为
mgv(sinθ-μcosθ)1 4
C.导体棒两端电压为mgR(sinθ-μcosθ) 2BL
D.t时间内通过导体棒的电荷量为mgt(sinθ-μcosθ) BL 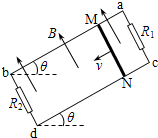
电磁感应的过程中,该电路的等效电路如图:
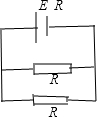
R外=R 2
导体棒下滑时产生的电动势:E=BLv
流过导体棒的电流:I=
=E R+R外
①2BLv 3R
A:导体棒匀速运动时,合力为零,即:mgsinθ=μmgcosθ+BIL ②
联立①②解得:v=
,故A错误;3mgR(sinθ-μcosθ) 2B2L2
B:导体棒的重力的功率:PG=mgvsinθ,摩擦力的功率:Pf=μmgcosθ•v,MN上的功率:PMN=I2R,R1R2上的功率:PR=(
I)2•R=1 2
I2R=1 4
PMN1 4
重力的功转化为摩擦力的功和导体棒、电阻R1、R2是的功.即:PG=Pf+PMN+2PR,
所以:PR=
mgv(sinθ-μcosθ).故B错误;1 6
C:导体棒两端的电压:U=I•R外=
BLv=1 3
.故C正确;mgR(sinθ-μcosθ) 2BL
D:t时间内通过的电量:q=It=
•t=2BLv 3R
.故D正确.mg(sinθ-μcosθ) BL
故选:CD
