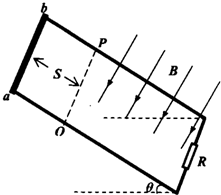
如图所示,有一足够长的光滑平行金属导轨,电阻不计,间距L=0.5m,导轨沿与水平方向成θ=30°倾斜放置,底部连接有一个阻值为R=3Ω的电阻.现将一根长也为L质量为m=0.2kg、电阻r=2Ω的均匀金属棒,自轨道顶部静止释放后沿轨道自由滑下,下滑中均保持与轨道垂直并接触良好,经一段距离后进入一垂直轨道平面的匀强磁场中,如图所示.磁场上部有边界OP,下部无边界,磁感应强度B=2T.金属棒进入磁场后又运动了一段距离便开始做匀速直线运动,在做匀速直线运动之前这段时间内,金属棒上产生了Qr=2.4J的热量,且通过电阻R上的电荷量为q=0.6C,取g=10m/s2.求:
(1)金属棒匀速运动时的速v0;
(2)金属棒进入磁场后,当速度v=6m/s时,其加速度a的大小及方向;
(3)磁场的上部边界OP距导轨顶部的距离S.
(1)根据平衡条件得F安=mgsinθ
又F安=BIL,I=
,E=BLv0E R+r
得到F安=B2L2v0 R+r
联立解得
v0=
=5m/smg(R+r)sinθ B2L2
(2)由牛顿第二定律,得
mgsinθ-F安=ma
得到a=gsinθ-
=-1m/s2 B2L2v m(R+r)
说明此时加速度大小为1m/s2,方向沿斜面向上.
(3)由于金属棒r和电阻R上电流时刻相同,由焦耳定律Q=I2Rt,得知Q∝R
则R产生的热量为QR=
Qr=3.6JR r
金属棒匀速运动整个电路产生的总热量Q=QR+Qr=6J
在该过程中电路的平均电流为I=
=E R+r △φ △t(R+r)
设匀速前金属棒在磁场中位移为x,则此过程中通过R的电量为q=I•△t=
=△φ R+r BLx R+r
从释放到刚匀速运动过程中,由能量守恒定律得
mgsinθ(S+x)=
m1 2
+Qv 20
联立上式,解得S=
-m
+2Qv 20 2mgsinθ
=5.5mq(R+r) BL
答:(1)金属棒匀速运动时的速v0为5m/s;
(2)金属棒进入磁场后,当速度v=6m/s时,加速度大小为1m/s2,方向沿斜面向上;
(3)磁场的上部边界OP距导轨顶部的距离S为5.5m.
