问题
填空题
已知集合A={(x,y)||x|+|y|=4,x,y∈R},B={(x,y)|x2+y2=r2,x,y∈R},若A∩B中的元素所对应的点恰好是一个正八边形的八个顶点,则正数r的值为______.
答案
根据题意,对于A,
x≥0,y≥0时,有x+y=1,
x≥0,y<0时,有x-y=1,
x<0,y≥0时,有x-y=-1,
x<0,y<0时,有x+y=-1,
故A表示由x+y=1,x+y=-1,x-y=1,x-y=-1围成的正方形,
而B表示一个圆心在原点,半径为r的圆,
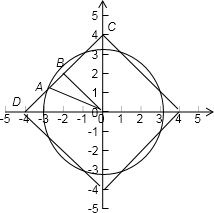
若A∩B中的元素所对应的点恰好是一个正八边形的八个顶点,如图,
则OA=r,OD=4,
易得OB=2
,2
∠BOA=
,π 8
有r=
.2 2 cos π 8
故答案为r=
.2 2 cos π 8
