问题
解答题
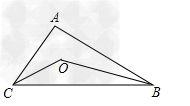
△ABC中，∠ABC、∠ACB的平分线相交于点O。
（1）若∠ABC=40°，∠ACB=50°，则∠BOC=________；
（2）若∠A=76°，则∠BOC=_________；
（3）若∠BOC=120°，则∠A=_________；
（4）你能找出∠A与∠BOC 之间的数量关系吗？
答案
解：（1）∵CO、BO分别是∠ABC、∠ACB的平分线，
∴∠OCB=
∠ACB=25°，∠OBC=
∠ABC=20°，
∴∠BOC=180°-（∠OCB+∠OBC）=180°-（20°+25°）=135°；
（2）∵CO、BO分别是∠ABC、∠ACB的平分线，
∴∠OCB=
∠ACB，∠OBC=
∠ABC，
∴∠BOC=180°-（∠OCB+∠OBC）=180°-
（∠ACB+∠ABC），
又∵∠ACB+∠ABC=180°-∠A=104°，
∴∠BOC=180°-
?104°=128°；
（3）∵∠BOC=120°，
∴∠OCB+∠OBC=60°，
∵∠OCB=
∠ACB，∠OBC=
∠ABC，
∴∠ABC+∠ACB=2（∠OCB+∠OBC）=120°，
∴∠A=60°；
（4）∠BOC=180°-（∠OCB+∠OBC）
=180°-
（∠ACB+∠ABC）
=180°-
（180°-∠A）
=90°+
∠A。
