问题
计算题
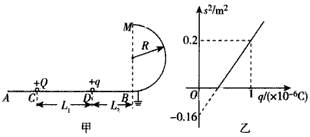
光滑绝缘水平面AB上有C,D两点。CD长L1=12 cm,DB长L2=9 cm。另有一半径R=0.1 m的光滑半圆形金属导轨BM与水平面平滑相连,金属导轨BM接地,连接处能量无损失。现将一个带电荷量为+Q的点电荷,固定在C点,如图甲所示。将另一带电荷量为+q,质量m=1×10-4 kg的金属小球(视为点电荷)从D点静止释放(感应电荷的影响忽略不计),若小球过圆弧的最高点后恰能击中C处的点电荷,重力加速度g=10 m/s2。
(1)求小球在最高点M时对轨道压力的大小;
(2)若不改变小球的质量而改变小球的电荷量+q,发现小球落地点到B点的水平距离s2与小球的电量+q满足图象乙的关系,求点电荷+Q的电场在DB两点的电势差UDB。
答案
解:(1)小球进入半圆形金属轨道后,电荷量变为零。小球从最高点水平抛出能击中C点,设速度为v,有
水平方向L1+L2=vt
竖直方向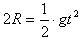
可得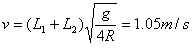
设最高点压力为FN,有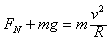
得FN=1.025×10-4 N
(2)设D,B电势差为UDB,带电小球从开始运动,到金属轨道最高点的过程中,由动能定理得
飞出后,由平抛运动规律有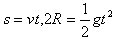
整理得函数关系为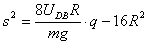
由图象得当q=0时,纵轴截距为s2=-16R2
斜率为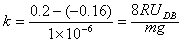
求得电势差UDB=450 V
