问题
计算题
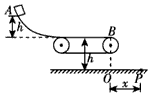
如图所示,光滑弧形轨道下端与水平传送带上表面等高,轨道上的A点到传送带的竖直距离和传送带上表面到地面的距离均为h=5 m。把一物体放在A 点由静止释放,当传送带不动,物体从右端B点水平飞离,落在水平地面上的P点,B,P的水平距离OP为x=2 m。g取10 m/s2,求:
(1)当传送带不动,物体飞出B点时的速度;
(2)若传送带以v=5 m/s的速度顺时针方向传送,物体会落在何处?
答案
解:(1)当传送带不动时,设物体进入和飞出传送带的速度分别为v1,v2
根据机械能守恒定律有 ,解得v1=10 m/s
,解得v1=10 m/s
物体离开B:由 ,解得t2=1 s
,解得t2=1 s

(2)因为v2<v<v1,所以物体先减速后匀速
飞出B点速度v2'=v=5 m/s
解得x'=v'2t2=5 m
