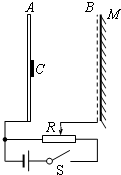
如图所示,在铅板A上放一个放射源C,可向各个方向射出速率为v的β射线,B为金属网,A、B连接在电路上,电源电动势为E,内阻为r,滑动变阻器的总阻值为R.图中滑动变阻器滑片置于中点,AB间的间距为d,M为足够大的荧光屏,M紧挨着金属网外侧.已知β粒子质量为m,电量为e.不计β射线所形成的电流对电路的影响,求:
(1)闭合开关S后,AB间场强的大小是多少?
(2)β粒子到达金属网B的最长时间是多少?
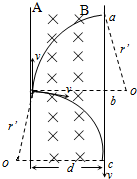
(3)切断开关S,并撤去金属B,加上垂直纸面向里、范围足够大的匀强磁场,磁感应强度为B,设加上磁场后β粒子仍能到达荧光屏,这时在荧光屏上发亮区的长度是多少?
(1)由闭合电路欧姆定律得:I=E R+r
UAB=
=IR 2 ER 2(R+r)
由EAB=
=UAB d ER 2(R+r)d
(2)β粒子在两板间运动只受电场力作用,
其加速度为a=
=F m
=eEAB m eER 2(R+r)dm
分析可知,沿A板方向射出的β粒子做类平抛运动到达B板所用时间最长.
根据:d=
at21 2
所以t=
=2d2d a m(R+r) eER
(3)β粒子垂直进入磁场只受洛伦兹力做匀速圆周运动,则有:
evB=mv2 r′
得r′=mv eB
荧光亮斑区的上边界就是沿A板射出的β粒子所达的a点
有:(r′-d)2+
2=r′2. ab
解得,l1=
=. ab
=d(2r′-d) d(
-d)2mv eB
荧光亮斑区的下边界就是β粒子轨迹与屏相切的C点(做轨迹图)
有:(r′-d)2+
2=r′2. bc
解得,l2=
=. bc d(
-d)2mv eB
在竖直方向上亮斑区的长度为l=l1+l2=2
=2d(2r′-d) d(
-d)2mv eB
答:
(1)闭合开关S后,AB间场强的大小是
.ER 2(R+r)d
(2)β粒子到达金属网B的最长时间是2d
.m(R+r) eER
(3)在荧光屏上发亮区的长度是2
.d(
-d)2mv eB