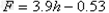如图所示,一质量m=0.1kg、电量q=1.0×10-5 C的带正电小球(可视作点电荷),它在一高度和水平位置都可以调节的平台上滑行一段距离后平抛,并沿圆弧轨道下滑。A、B为圆弧两端点,其连线水平,已知圆弧半径R=1.0m,平台距AB连线的高度h可以在0.2m-0.8m之间调节。有一平行半径OA方向的匀强电场E,只存在圆弧区域内。为保证小球从不同高度h平抛,都恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,小球平抛初速度v0和h满足如图所示的抛物线,同时调节平台离开A点的距离合适。不计空气阻力,取g=10m/s2,求:
(1)小球在空中飞行的最短时间t;
(2)平台离开A的水平距离x范围;
(3)当h=0.2m且E=2.5×104N/C时,小球滑到最低点C点的速度v;
(4)为了保证小球在圆轨道内滑动到C点的速度都是(3)中的v,则电场力F=qE的大小应与平台高度h满足的关系。(通过列式运算说明)

解:(1)当平台高度为0.2m时,空中飞行的最短时间t=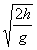 =0.2s
=0.2s
(2)因为小球从不同高度h平抛,都恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,所以小球进入圆弧轨道时时的速度方向不变,设此速度与竖直方向成α角
tgα=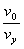 =
=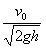
v02=2ghtan2α
由图像中当h=0.8m时,v0=3m/s代入上式得
9=2×10×0.8×tg2α
tgα=0.75,α=37°,则θ=106°
所以v02=11.25h
当h=0.2m时,v0=1.5m/s
平台离开A的最小距离为s1=v0t=1.5×0.2=0.3m
同理得平台离开A的最大距离为s2= v0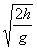 =3×
=3× =1.2m
=1.2m
(3)小球到达A点时的速度vA=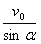 =
=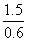 =2.5m/s
=2.5m/s
从A点到C点,由动能定理得mgR(1-cos53°)-qER(1-cos53°)=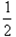 mvC2-
mvC2-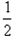 mvA2
mvA2
代入数据,解得vC=3.5m/s
(4)从A点到C点,由动能定理得
mgR(1-cos53°)-FR(1-cos53°)=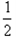 mvC2-
mvC2-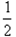 mvA2=
mvA2=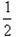 mvC2-
mvC2-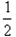 m
m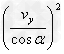 =
=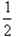 mvC2-
mvC2-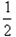 m
m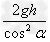
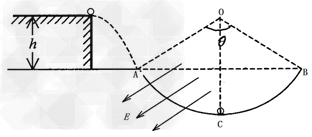
代入数据得32F=125h-17
或