问题
填空题
顶角为60°的等腰三角形，两个底角的平分线相交所成的角是______°．
答案
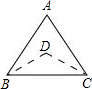
如图所示：
因为△ABC是等腰三角形且∠A=60°，所以∠ABC=∠ACB=60°，
又因为BD，CD分别平分∠ABC和∠ACB，
所以∠DBC=∠DCB=30°，所以∠BDC=120°，
所以两个底角的平分线相交所成的角是60°或120°．
故答案为：60或120
搜题请搜索小程序“爱下问搜题”
顶角为60°的等腰三角形，两个底角的平分线相交所成的角是______°．
如图所示：
因为△ABC是等腰三角形且∠A=60°，所以∠ABC=∠ACB=60°，
又因为BD，CD分别平分∠ABC和∠ACB，
所以∠DBC=∠DCB=30°，所以∠BDC=120°，
所以两个底角的平分线相交所成的角是60°或120°．
故答案为：60或120