问题
计算题
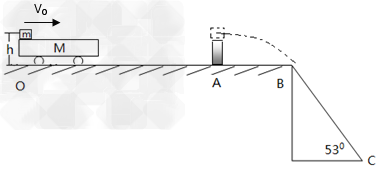
工厂里有一种运货的过程可以简化为如图所示,货物m=20kg,以初速度V0=10m/s滑上静止的小车M,M=30kg,货车高h=0.8m。在光滑的轨道OB上设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点,已知货车上表面的动摩擦因数μ=0.5,斜面的倾角为53°(sin53°=0.8,cos53°=0.6,g=10m/s2)
(1)求货物从A到B点的时间;
(2)求AB之间的水平距离;
(3)若已知OA段距离足够长,导致货车在碰到A之前已经与货物达到共同速度,则货车的长度是多少?
答案
解:(1)货物从小车上滑出之后做平抛运动,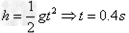 ……(1)
……(1)
(2)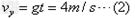
在B点分解速度,如图: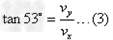
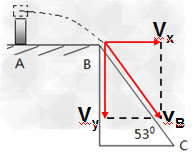
得:
故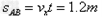
(3)在小车碰撞到障碍物前,车与货物已经到达共同速度根据动量守恒定律:
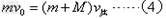
得: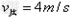
根据系统能量守恒定律: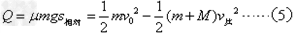
联立(4)(5)解得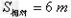
当小车被粘住之后,物块继续在小车上滑行,直到滑出根据动能定理:

解得s'=0.7m
故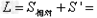 6.7m
6.7m
