问题
计算题
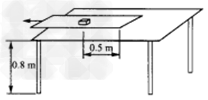
如图所示，静止放在水平桌面上的纸带，其上有一质量为m=0.1 kg的铁块，它与纸带右端的距离为L=0.5m，所有接触面之间的动摩擦因数相同。现用水平向左的恒力，经2s时间将纸带从铁块下抽出，当纸带全部抽出时铁块恰好到达桌面边缘且速度为v=2m/s。已知桌面高度为H=0.8m，不计纸带重力，铁块视为质点。重力加速度g取10m/s2，求：
（1）铁块抛出后落地点离抛出点的水平距离；
（2）动摩擦因数；
（3）纸带抽出过程中系统产生的内能。
答案
解：（1）设铁块离开桌面后经时间t落地
水平方向：x＝vt ①
竖直方向：H＝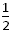
gt2 ②
由①②联立解得：x=0.8 m
（2）设铁块的加速度为a1，运动时间为t1，由牛顿第二定律，得μmg＝ma1 ③
纸带抽出时，铁块的速度v＝a1t1 ④
③④联立解得μ=0.1
（3）铁块的位移x1＝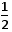
a1t12 ⑤
设纸带的位移为x2；由题意知，x2－x1＝L ⑥
由功能关系可得纸带抽出过程中系统产生的内能E＝μmgx2＋μmgL ⑦
由③④⑤⑥⑦联立解得E＝0.3 J