如图所示，半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内，轨

问题问答题

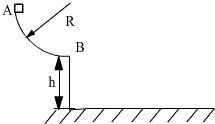
如图所示，半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内，轨道的B端切线水平，且距水平地面高度为h=1.25m，现将一质量m=0.2kg的小滑块从A点由静止释放，滑块沿圆弧轨道运动至B点以v=5m/s的速度水平飞出（g取10m/s²）．求：

（1）小滑块沿圆弧轨道运动过程中所受摩擦力做的功；

（2）小滑块经过B点时对圆轨道的压力大小；

（3）小滑块着地时的速度大小．

答案

（1）设小滑块沿圆弧轨道运动过程中所受摩擦力做的功为W_f，应用动能定理研究A点到B点有：

mgR+W_f=

mv^{2
解得W_f=-1.5J．
（2）对B点进行受力分析，设轨道对滑块的支持力为N，由牛顿第二定律有：
N-mg=m
v2
R
解得N=4.5N
由牛顿第三定律知滑块对B的压力为4.5N，方向竖直向下．
（3）滑块过B点后作平抛运动，设着地时竖直速度为v_y，
根据平抛运动规律有：
竖直方向末速度v_y=
2gh
=5m/s
所以v=
v2+v 2y
=5
2m/s
答：（1）小滑块沿圆弧轨道运动过程中所受摩擦力做的功为-1.5J；
（2）小滑块经过B点时对圆轨道的压力大小为4.5N；
（3）小滑块着地时的速度大小是5
2
m/s．}