(16分)面粉增白剂主要包括过氧化苯甲酰(俗称面粉增白剂)和过氧化钙两种物质。其中过氧化钙(CaO2)在日常生活和工农业生产中还常用于种子消毒、药物制造、油脂漂白及鱼池增氧等,还可以作为高温氧化剂。已知:过氧化钙与CO2反应有气体生成,而将SO2通入过氧化钙粉末中也有气体生成。有人提出CO2、SO2与过氧化钙的反应原理相同,但也有人提出SO2具有较强的还原性,CO2无强还原性,反应原理不相同。据此设计如下实验操作进行判断。
实验一:通过测量气体的体积判断发生的化学反应,实验装置如下:
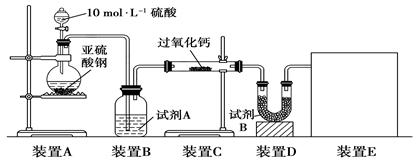
(1)试剂A可以选用________,试剂B的作用是________。
(2)装置E用于测定氧气的体积,请在方框中画出装置图。
(3)实验测得装置C中过氧化钙质量增加了m1 g,装置D质量增加了m2 g,装置E中收集到的气体为V L(已换算成标准状况下),用上述有关测量数据判断,SO2未被氧化、部分被氧化、完全被氧化的V——m1关系式。
未被氧化:____________,部分被氧化:____________,
完全被氧化:____________。
若SO2完全被氧化,写出反应的化学方程式:___________________________。
实验二:向一定量的过氧化钠固体中通入足量的SO2,取反应后的固体进行实验探究,以证明过氧化物与SO2反应的特点。
提出假设:
假设1:反应后固体只有________,证明SO2未被氧化;
假设2:反应后固体中只有________,证明SO2完全被氧化;
假设3:________________________________________________________。
实验探究:
(4)设计实验,证明假设3是正确的,简要回答实验过程、现象和结论:______
_____________________________________________________________。
实验评价:
(5)实验过程中SO2的通入量直接影响探究实验结果的科学性,请简要说明原因:___________________________________________________________。