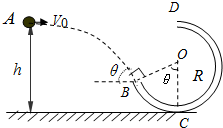
如图所示,竖直平面内有一光滑圆弧轨道,其半径R=0.5m.一质量m=1.0kg的小球(可以看成质点)从离地高度h=1.0m的A点水平射出,恰能沿圆弧轨道上B点的切线方向进入轨道内侧,轨道半径OB与竖直线的夹角θ=53°.已知:sin53°=0.8,cos53°=0.6,g取10m/s2.试求:
(1)小球从A点到B点的时间t;小球从A点水平射出时的速度大小V0;
(2)小球从射出点A到圆轨道入射点B之间的距离L;(结果可用根式表示)
(3)小球沿轨道通过圆弧的最高点D时对轨道的压力大小和方向.
(1)B点的高度 hB=R(1-cos53°)=0.2m
A到B:h-hB=
gt2,t=0.4s 1 2
在B点的竖直速度 Vy=gt=4 m/s
水平速度 V0=Vycot53°=3m/s
(2)A到B的水平距离:x=V0t=1.2m
A到B的距离:L=
=x2+(h-hB)2
m2.08
(3)A到D过程中,由机械能守恒定律得:
VD=V0=3 m/s
小球重力 mg=10 N
在D点的向心力 FA=m
=18Nv2 R
小球受到轨道的弹力FD=FA-mg=8 N 竖直向下
由牛顿第三定律可得,小球在D点时对轨道的压力为:
FD′=FD=8 N 竖直向上
答:(1)小球从A点到B点的时间为0.4s;小球从A点水平射出时的速度大小为3m/s;
(2)小球从射出点A到圆轨道入射点B之间的距离L为
m;2.08
(3)小球沿轨道通过圆弧的最高点D时对轨道的压力大小为8N和,方向竖直向上.
