问题
问答题
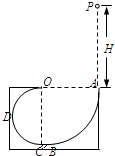
如图所示,ABCDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的
圆周轨道,CDO是直径为15m的半圆轨道.AB和CDO通过极短的水平轨道(长度忽略不计)平滑连接.半径OA处于水平位置,直径OC处于竖直位置.一个小球P从A点的正上方高H处自由落下,从A点进入竖直平面内的轨道运动(小球经过A点时无机械能损失).当小球通过CDO轨道最低点C时对轨道的压力等于其重力的1 4
倍,(取g为10m/s2).23 3
(1)试求高度H的大小?
(2)试讨论此球能否到达CDO轨道的最高点O,并说明理由?
(3)求小球沿轨道运动后经多长时间再次落回轨道上?
答案
(1)设小球通过D点的速度为v,则有:
m
=F=v2 R 2
mg14 3
小球从P点落下直到沿光滑轨道运动的过程中,机械能守恒,有mg(H+
)=R 2
mv21 2
可得高度H=
R=10m2 3
(2)设小球能够沿竖直半圆轨道运动到O点的最小速度为vc,有m
=mgvC2 R 2
小球至少应从Hc高处落下,mgHC=
mvC21 2
解得HC=
由H>HC,小球可以通过O点.R 4
(3)小球由H落下通过O点的速度为v0=
=14.1m/s2gH
小球通过O点后作平抛运动,设小球经时间t落到AB圆弧轨道上,有
x=v0t
y=
gt2 1 2
且x2+y2=R2
可解得时间t=1s (另解舍弃)
答:(1)高度H的大小为10m;
(2)能到达CDO轨道的最高点O;
(3)小球沿轨道运动后经1s再次落回轨道上.
