问题
问答题
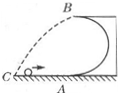
如图所示,一半径为R的光滑半圆形轨道AB固定在水平地面上,一个质量为m的小球以某一速度从半圆形轨道的最低点A冲上轨道,当小球将要从轨道最高点B飞出时,小球对轨道的压力为3mg(g为重力加速度),求
(1)小球在半圆形轨道最高点时的加速度大小.
(2)小球达到B点时的速度大小.
(3)小球的落地点C离A点的水平距离.
答案
(1)当小球在B点时由向心力的公式可得 N+mg=ma,
所以 3mg+mg=ma,
解得a=4g;
(2)当小球在B点时由向心加速度的公式可得a=
,v 2B R
所以 4g=v 2B R
解得VB=2gR
(3)小球从B点飞出后,做平抛运动,运动的时间是t:
由 2R=
gt21 2
所以 t=2
,R g
小球落地点到A点的距离:x=VBt=2
×2gR
=4RR g
答:(1)小球在半圆形轨道最高点时的加速度大小为4g;
(2)小球达到B点时的速度大小为2
;gR
(3)小球的落地点C离A点的水平距离为4R.
