已知:一次函数y=3x-2的图象与某反比例函数的图象的一个公共点的横坐标为1.
(1)(3分)求该反比例函数的解析式;
(2)(3分)将一次函数y=3x-2的图象向上平移4个单位,求平移后的图象与反比例函数图象的交点坐标;
(3)(2分)请直接写出一个同时满足如下条件的函数解析式:
①函数的图象能由一次函数y=3x-2的图象绕点(0,-2)旋转一定角度得到;
②函数的图象与反比例函数的图象没有公共点.
(1) (2)交点坐标为(
(2)交点坐标为( ,3)和(-1, -1) (3)y=-2x-2(答案不唯一)
,3)和(-1, -1) (3)y=-2x-2(答案不唯一)
解:(1)把x=1代入y=3x-2,得y=1。
设反比例函数的解析式为 ,把(1,1)代入得,k=1。
,把(1,1)代入得,k=1。
∴该反比例函数的解析式为
(2)平移后的图象对应的解析式为y=3x-2+4,即y=3x+2,
联立y=3x+2和 ,得,
,得,
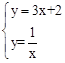 ,解得
,解得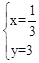 或
或 。
。
∴平移后的图象与反比例函数图象的交点坐标为( ,3)和(-1, -1) 。
,3)和(-1, -1) 。
(3)y=-2x-2(答案不唯一)。
(1)先求出两函数的交点坐标,利用待定系数法即可求得反比例函数的解析式。
(2)平移后的图象对应的解析式为y=3x+2,联立两函数解析式,从而求得交点坐标。
(3)∵函数的图象由一次函数y=3x-2的图象绕点(0,-2)旋转一定角度得到,
∴可设所求函数解析式为y=mx-2,则由
 得
得 。
。
∵函数的图象与反比例函数的图象没有公共点,
∴△=4-4·m(-1)<0,解得m<-1。
∴只要常数项为-2,一次项系数小于-1的一次函数均可。
