问题
选择题
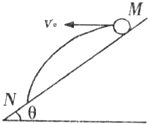
如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则(重力加速度为g)( )
A.可求M、N之间的距离
B.可求小球落到N点时速度的大小和方向
C.可求小球到达N点时的动能
D.可以断定,当小球速度方向与斜面平行时,小球与斜面间的距离最大
答案
A、已知位移的与水平方向之间的夹角为θ,而由平抛运动的规律可知,tanθ=
=
gt21 2 v0t
,可求得时间为t=gt 2v0
,即可求得竖直位移,再由几何关系可求得MN间的距离,故A正确;2v0tanθ g
B、由vy=gt,可求得竖直分速度,由速度的合成与分解可求得最后末速度的大小和方向,故B正确;
C、已求出小球的速度,但不知小球的质量,故无法求出小球的动能,故C错误;
D、将初速度沿斜面和垂直于斜面进行分解,同时将加速度也同方向分解;当垂直于斜面的速度为零时,小球距离斜面最远,故D正确.
故选ABD

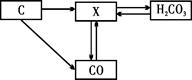
 2Cu + X↑体现了碳的还原性
2Cu + X↑体现了碳的还原性