问题
问答题
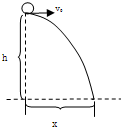
一宇航员在某未知星球的表面上做平抛运动实验:在离地面h高处让小球以v0的初速度水平抛出,他测出小球落地点与抛出点的水平距离为x,又已知该星球的半径为R,己知万有引力常量为G,求:
(1)小球从抛出到落地的时间t
(2)该星球表面的重力加速度g
(3)该星球的质量M
(4)该星球的第一宇宙速度v
(最后结果必须用题中己知物理量表示)
答案
(1)小球做平抛运动,
在水平方:X=V0t,
解得:从抛出到落地时间为:t=
;x v0
(2)小球做平抛运动时在竖直方向上有:h=
gt2,1 2
解得,该星球表面的重力加速度为:g=
=2h t2
;2h v 20 x2
(3)设地球的质量为M,静止在地面上的物体质量为m,
由万有引力等于物体的重力得:mg=
,GMm R2
所以该星球的质量为:M=
=gR2 G
;2h
R2v 20 Gx2
(4)设有一颗质量为m的近地卫星绕地球作匀速圆周运动,速率为v,
由牛顿第二定律得:
=GMm R2
,mv2 R
重力等于万有引力,即mg=
,GMm R2
解得,该星球的第一宇宙速度为:v=
=gR v0 x
;2hR
答:(1)小球从抛出到落地的时间t=
;x v0
(2)该星球表面的重力加速度g=
;2h v 20 x2
(3)该星球的质量M=
;2h
R2v 20 Gx2
(4)该星球的第一宇宙速度v=v0 x
.2hR
