问题
选择题
根据经典理论,金属导体中电流的微观表达式为I=nvSe,其中n为金属导体中每单位体积内的自由电子数,v为导体中自由电子沿导体定向移动的速率,S为导体的横截面积,e为自由电子的电荷量.如图11所示,两段长度和材料完全相同、各自粗细均匀的金属导线ab、bc,圆横截面的半径之比为rab∶rbc=1∶4,串联后加上电压U,则 ( )
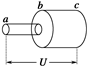
A.两导线内的自由电子定向移动的速率之比为vab∶vbc=1∶4
B.两导线内的自由电子定向移动的速率之比为vab∶vbc=4∶1
C.两导线的电功率之比为Pab∶Pbc=4∶1
D.两导线的电功率之比为Pab∶Pbc=16∶1
答案
答案:D
因两段串联,通过两棒的电流相等,又I=neSv,故neπr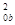 vab=neπr
vab=neπr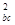 vbc,得vab∶vbc=16∶1,A、B均错.由电阻定律Rab=ρ
vbc,得vab∶vbc=16∶1,A、B均错.由电阻定律Rab=ρ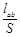 =ρ
=ρ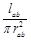 ,Rbc=ρ
,Rbc=ρ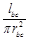 ,求得Rab∶Rbc=16∶1,因为ab和bc串联,流过两段的电流相等,由功率公式P=I2R,得Pab∶Pbc=Rab∶Rbc=16∶1,故D正确,C错误.
,求得Rab∶Rbc=16∶1,因为ab和bc串联,流过两段的电流相等,由功率公式P=I2R,得Pab∶Pbc=Rab∶Rbc=16∶1,故D正确,C错误.

