问题
填空题
在△ABC中,已知∠A=80°,则∠B、∠C的角平分线相交所成的钝角为______.
答案
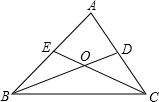
如图,∵∠A=80°,
∴∠ABC+∠ACB=180°-80°=100°,
∵BD、CE分别是∠B、∠C的角平分线,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=1 2
×100°=50°,1 2
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°,
所以,∠B、∠C的角平分线相交所成的钝角为130°.
故答案为:130°.