如图所示，质量均为m的A、B两个弹性小球，用长为2l的不可伸长的

问题问答题

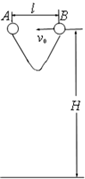
如图所示，质量均为m的A、B两个弹性小球，用长为2l的不可伸长的轻绳连接．现把A、B两球置于距地面高H处（H足够大），间距为l，当A球自由下落的同时，B球以速度v_o指向A球水平抛出．求：

（1）两球从开始运动到相碰，A球下落的高度．

（2）A、B两球碰撞（碰撞时无机械能损失）后，各自速度的水平分量．

（3）轻绳拉直过程中，B球受到绳子拉力的冲量大小．

答案

（1）设 A球下落的高度为h

l=v₀t…..①

gt²…②

联立①②得：

gl2

…③

（2）由水平方向动量守恒得：

mv₀=mv'_Ax+mv'_Bx…④

由机械能守恒得：

m（v²₀+v²_By）+

mv²_Ay=

m（v

′

2AX

′

2Ay

）+

m（v

′

2Bx

′

2By

）

式中v′_Ay=v_Ay v′_By=v_By

联立④⑤得：

v_′Ax=v₀

v′_Bx=0

（3）由水平方向动量守恒得：

mv₀=2m v′_Bx

I=mv″_Bx=

mv_{0
答：（1）A球下落的高度
gl2
2v 20
；
（2）v_′Ax=v₀，v′_Bx=0，
（3）轻绳拉直过程中，B球受到绳子拉力的冲量
1
2
mv0}